Sehschärfebestimmung nach Europäischer Norm
Wissenschaftliche Grundlagen und Möglichkeiten der automatischen MessungMichael Bach und Guntram Kommerell
Vorläufiges Manuskript, endgültige Version erschien in: Klinische Monatsblätter für Augenheilkunde (1998; 212:190-195), Ferdinand Enke-Verlag
Nachträgliche Erweiterungen: Spalte 7 in Tab. 1 (24.4.2002)
Zusammenfassung
Bei der Ermittlung der Sehschärfe sollten dem Augenarzt die wissenschaftlichen Grundlagen gegenwärtig sein, auch wenn er aus praktischen Erwägungen in vielen Fällen ein Verfahren wählen kann, das strengen theoretischen Forderungen nicht genügt.
Psychometrische Funktion. In der Europäischen Norm EN ISO 8596 (wie auch in der früher gültigen DIN 58220) ist für die Messung der Sehschärfe der Landoltring vorgeschrieben, der in 8 verschiedenen Orientierungen anzubieten ist. Bei abnehmender Größe des Landoltrings sinkt die Trefferrate von 100% auf die Ratewahrscheinlichkeit (Zufallswahrscheinlichkeit) von 12,5%. Dieser allmähliche Übergang wird durch die "psychometrische Funktion" beschrieben. In Kurvenform dargestellt hat die psychometrische Funktion eine steilste Stelle (=Wendepunkt). Sie liegt in der Mitte zwischen 100 und 12,5, also bei einer Trefferrate von 56,25%. Diese steilste Stelle (angenähert durch 5 von 8 Landoltringen) wurde als Schwelle gewählt, weil die dort abgelesene Sehschärfe von zufälligen Schwankungen am wenigsten beeinflusst wird.
Forced choice. Der Proband muss bei der Benennung der Landoltring-Orientierung zu "forced choice" angehalten werden; eine Aussage wie "ich kann gar nichts erkennen" darf nicht akzeptiert werden.
"Normale" Sehschärfe. Sie kann nicht einer bestimmten Zahl zugeordnet werden, wie etwa 1,0; bei normgerechter Prüfung erreichen junge, augengesunde Probanden Werte um 2,0, während bei alten Probanden 0,5 "normal" sein kann.
Mittelung der Sehschärfe. Nur bei logarithmischer, nicht bei arithmetischer Skalierung der Sehschärfe ergeben sich etwa gleiche, der Empfindungsstärke entsprechende Stufen. Daher dürfen Sehschärfewerte auch nicht arithmetisch gemittelt werden. Korrekt ist es dagegen, geometrisch zu mitteln bzw. die Sehschärfewerte zunächst zu logarithmieren, dann zu mitteln und schließlich den erhaltenen Wert zu delogarithmieren.
"Minimum Angle of Resolution" überflüssig. MAR ist der Kehrwert der Sehschärfe. Die neuerdings zuweilen gewählte Kennzeichnung des Auflösungsvermögens mit log(MAR) ist überflüssig, denn log(MAR) hat die selben statistischen Eigenschaften wie log(Sehschärfe). Zudem ist log(MAR) unanschaulich, da der Wert bei Zunahme des Sehvermögens abnimmt.
Computergestützte Verfahren. Sie erleichtern das Befolgen der EN ISO 8596. So muss sich der Untersucher z.B. beim "Freiburger Visustest" nicht selbst merken, ob pro Stufe bereits 5 richtige Antworten gegeben wurden, und er muss nicht darauf achten, dass der Landoltring pro Stufe höchstens 8 mal angeboten wird.
Einleitung
Anliegen dieses Artikels ist es, die wissenschaftlichen Grundlagen der Sehschärfebestimmung darzustellen, auf denen die EN ISO 8596 (Europäische Norm, CEN (Europäisches Komitee für Normung) 1996) beruht. Die EN ISO entspricht weitgehend der früher gültigen DIN 54220. Bei der Ermittlung der Sehschärfe (=Visus) sollten dem Augenarzt die wissenschaftlichen Grundlagen gegenwärtig sein, auch wenn er aus praktischen Erwägungen in vielen Fällen ein Verfahren wählen kann, das strengen theoretischen Forderungen nicht genügt.
Alle nachstehenden Überlegungen folgen aus der Auffassung der Sehschärfe als psychophysische Schwelle: Ein physisches Maß (die Optotypengröße) wird zur Wahrnehmung in Beziehung gesetzt, und an geeigneter Stelle wird eine Schwelle definiert. Nach EN ISO wird die Sehschärfe mit Landoltringen gemessen. Sie ergibt sich aus der Formel (z.B. Paliaga 1993)
Sehschärfe = 1/Lücke des kleinsten erkannten Landoltrings [Bogenminuten].
Logarithmische Abstufung der Sehschärfe
Die Abstufung zwischen den einzelnen Sehschärfewerten entspricht nur dann der Empfindungsstärke, wenn logarithmisch skaliert wird (Ferris et al. 1982; Paliaga 1993). Warum dies so ist, kann man sich am besten an zwei Beispielen klar machen: Für einen Patienten, der nur über eine Sehschärfe von 0,1 verfügt, ist ein Anstieg um 0,1 auf 0,2 ein großer Gewinn, denn die Sehschärfe hat sich verdoppelt, und der Patient kann nun ein Schild aus einer doppelt so großen Entfernung lesen. Für einen Patienten mit der Sehschärfe 0,8 hingegen ist eine Erhöhung um 0,1 auf 0,9 praktisch unbedeutend, denn die Sehschärfe hat sich nur um den Faktor 0,908 = 1,125 verbessert. Aus diesen Beispielen geht hervor, dass die Sehschärfe nicht in arithmetisch gleichen Abständen, sondern geometrisch mit einem konstanten Faktor, also logarithmisch, skaliert sein sollte.
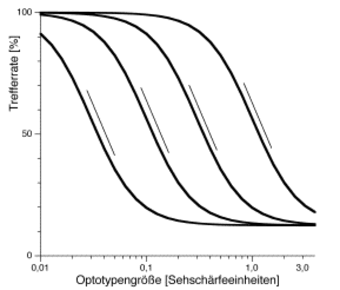
Psychometrische Funktionen bei 4 fiktiven Probanden unterschiedlicher Sehschärfe. Nur bei logarithmischer Skalierung der Sehschärfe verlaufen die psychometrischen Funktionen parallel (hier angedeutet durch Tangenten).
Psychometrische Funktion
Eine theoretische Begründung erfährt die logarithmische Skalierung durch die psychometrische Funktion (Abb. 1 und 2; Green and Swets 1966; Harvey 1986; Petersen 1993), die die Abhängigkeit der Wahrnehmung von der Reizstärke spezifiziert. Im Beispiel der Sehschärfe ist es die Abhängigkeit der Erkennungsrate von der Sehzeichengröße. Bei der Erkennungsrate handelt es sich um ein Wahrscheinlichkeitsmaß: Man bestimmt, mit welcher Häufigkeit eine bestimmte Optotype richtig benannt wird (Trefferrate). Von der 100% richtigen Benennung bei sehr großen Optotypen gibt es einen allmählichen Übergang zur Ratewahrscheinlichkeit bei ganz kleinen Optotypen. Die Steigung der psychometrischen Funktion ist bei verschieden gut sehenden Probanden nur dann annähernd gleich, wenn logarithmisch skaliert wird (Abb. 1; Westheimer 1979; Petersen 1990).
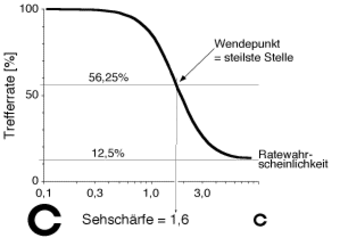
Für die Definition der Sehschärfe wird der Wendepunkt der psychometrischen Funktion herangezogen, da die psychometrische Funktion hier am steilsten ist. Zufällige Schwankungen der Trefferrate wirken sich an der steilsten Stelle auf die Sehschärfe am wenigsten aus. (Der Wendepunkt liegt bei 8 möglichen Darbietungen des Landoltrings bei einer Trefferrate von 56,25% (der Mitte zwischen 100 und 12,5%). Im dargestellten Beispiel beträgt die Sehschärfe 1,6.
Definition der Schwelle
Bei der Darstellung der psychometrischen Funktion in Kurvenform erkennt man einen Wendepunkt. Am Wendepunkt hat die Kurve ihre größte Steigung. Dies bedeutet, daß sich am Wendepunkt Änderungen der Trefferrate in besonders kleinen Änderungen der abgelesenen Sehschärfe ausdrücken und dass die Reproduzierbarkeit der Sehschärfebestimmung optimal ist, wenn man den Wendepunkt für die Definition der Schwelle benutzt (Petersen 1990). Die Europäische Norm EN ISO 8596 ist diesem Gesichtspunkt gefolgt. Sie verlangt, dass bei 8 möglichen Orientierungen des Landoltrings 5 von 8 Darbietungen richtig benannt werden.
Die Wahl der steilsten Stelle der psychometrischen Funktion als Kriterium bringt es mit sich, dass ein Landoltring, dessen Größe gerade der Sehschärfe entspricht, nur in ca. 60% der Abfragen richtig benannt wird, immerhin aber in ca. 40% falsch! Für den Patienten ist die Prüfung an der Schwelle unangenehm, weil die Landoltringe in diesem Bereich so klein angeboten werden, dass er leicht das Gefühl bekommen kann, nur zu raten. Der Untersucher muss um dieses Gefühl wissen und den Patienten zu bestmöglichem Raten ermuntern. Das Unsicherheitsgefühl des Patienten kontrastiert mit der in der Regel guten Reproduzierbarkeit des Ergebnisses. Doch sollte die Reproduzierbarkeit von Sehschärfemessungen realistisch eingeschätzt werden: Petersen (1993) fand, dass sich nur bei 1/3 aller Wiederholungen der selbe Sehschärfewert ergab; bei 1/6 aller Wiederholungen betrug der Unterschied sogar 2 Visusstufen (2 Zeilen nach oben oder unten in Tabelle 1).
Sehschärfebestimmung mit erzwungener Wahl (“forced choice”)
Um die Sehschärfe möglichst unbeeinflusst vom Temperament des Probanden zu messen, muss man von ihm bei jedem angebotenen Landoltring eine eindeutige Aussage über die Lage der Lücke verlangen. Würde man Antworten hinnehmen wie “den Ring kann ich nicht erkennen, er ist viel zu klein”, käme bei entscheidungsschwachen Patienten, die “bloß nichts falsch machen” wollen, eine zu niedrige Sehschärfe heraus. Um dies zu vermeiden, schreibt die EN ISO “forced choice” vor. Der Sinn leuchtet vielen Patienten nicht spontan ein, da sie zu der Annahme neigen, dass ein Ergebnis nicht stimmen kann, in das auch falsche Antworten eingeflossen sind. Es mag helfen, zu erklären, dass man eine “Grenze” dadurch besonders genau bestimmen kann, dass man sich ihr von beiden Seiten aus nähert.
Welche Sehschärfe ist “normal”?
Häufig wird eine Sehschärfe von 1,0 als normal angesehen, also das einer Bogenminute entsprechende Auflösungsvermögen. Die Wahl der Bogenminute als “Standard” für die Sehschärfe hat historische Gründe: Bei Sehzeichen wie dem Landoltring führte sie zu Werten, die bei Normalpersonen um 1,0 lagen. Zu diesen Werten kam man allerdings nur, da man 100% richtige Antworten verlangte. Bei dem modernen Messverfahren mit forced choice und Definition der Schwelle an der steilsten Stelle der psychometrischen Funktion ergibt sich bei augengesunden, jungen Probanden eine Sehschärfe um 2,0 (Rassow et al. 1990).
Bei hohen Sehschärfewerten wirkt zunächst irritierend, dass die Ergebnisse bei Wiederholung stark zu streuen scheinen, so zum Beispiel zwischen 1,6 und 2,5. Auf der physiologisch angemessenen logarithmischen Skala liegen jedoch 1,6 und 2,5 nur eine Stufe von 2,0 entfernt, also im gleichen Abstand wie 0,16 und 0,25 von 0,2. Um diesen Zusammenhang deutlich zu machen, ist die logarithmische Abstufung der Sehschärfe im Bereich zwischen 0,01 und 2,5 in Tabelle 1 wiedergegeben. Dabei wurde die Abstufung nach EN ISO so gewählt, dass gerade 10 Intervalle zwischen 0,1 und 1,0 liegen. Daraus ergibt sich eine Stufengröße (=Faktor) von 10. Wurzel aus 10 = 1,26.
Tabelle 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Visus [10. Wurzel aus 10-Stufen] |
Visus [DIN bzw. EN ISO] |
log (Visus) |
MAR (Lücke ['] des Landol- trings) |
log (MAR) |
Snellen, 6 m |
MARAN (adjusted meter vision) |
|
0,008 |
|
-2,1 |
|
2,1 |
|
|
|
0,0100 |
|
-2,0 |
100,0 |
2,0 |
|
|
|
0,0125 |
|
-1,9 |
79,4 |
1,9 |
|
|
|
0,0158 |
|
-1,8 |
63,1 |
1,8 |
|
|
|
0,0199 |
|
-1,7 |
50,1 |
1,7 |
|
|
|
0,0251 |
|
-1,6 |
39,8 |
1,6 |
|
|
|
0,0316 |
|
-1,5 |
31,6 |
1,5 |
|
|
|
0,0398 |
|
-1,4 |
25,1 |
1,4 |
|
|
|
0,0501 |
0,05 |
-1,3 |
20,0 |
1,3 |
|
|
|
0,0631 |
0,063 |
-1,2 |
15,8 |
1,2 |
|
|
|
0,0794 |
0,08 |
-1,1 |
12,6 |
1,1 |
|
|
|
0,1000 |
0,1 |
-1,0 |
10,0 |
1,0 |
6/60 |
|
|
0,1259 |
0,125 |
-0,9 |
7,9 |
0,9 |
6/48 |
|
|
0,1584 |
0,16 |
-0,8 |
6,3 |
0,8 |
6/38 |
|
|
0,1995 |
0,2 |
-0,7 |
5,0 |
0,7 |
6/30 |
|
|
0,2511 |
0,25 |
-0,6 |
4,0 |
0,6 |
6/24 |
|
|
0,3162 |
0,32 |
-0,5 |
3,2 |
0,5 |
6/20 |
|
|
0,3981 |
0,4 |
-0,4 |
2,5 |
0,4 |
6/15 |
|
|
0,5011 |
0,5 |
-0,3 |
2,0 |
0,3 |
6/12 |
|
|
0,6309 |
0,63 |
-0,2 |
1,6 |
0,2 |
6/10 |
|
|
0,7943 |
0,8 |
-0,1 |
1,3 |
0,1 |
6/7,5 |
|
|
1,0000 |
1,0 |
0,0 |
1,0 |
0,0 |
6/6 |
|
|
1,2589 |
1,25 |
0,1 |
0,79 |
-0,1 |
6/4,8 |
|
|
1,5848 |
1,6 |
0,2 |
0,63 |
-0,2 |
6/3,75 |
|
|
1,9952 |
2,0 |
0,3 |
0,50 |
-0,3 |
6/3 |
|
|
2,5118 |
|
0,4 |
0,40 |
-0,4 |
|
|
Sehschärfestufen.
Spalte 1: logarithmische Stufen im Abstand des Faktors 10. Wurzel 10=1,259.
Spalte 2: Aus Spalte 1 durch Rundung entstandene Werte nach EN ISO 8596.
Spalte 3: Logarithmus der Spalte 1; man sieht die Abstufung in 1/10-log-Einheiten.
Spalte 4: “Minimum Angle of Resolution” (MAR) in Bogenminuten = Kehrwert der Sehschärfe.
Spalte 5: Logarithmus der Spalte 4; wie bei log(Visus) erkennt man die 1/10-log-Stufen.
Spalte 6: Snellen-Buchstaben nach der Zuordnung von Ferris et al. (1982).
Spalte 7: Zuordnung nach dem MARAN-Protokoll
Sehschärfe in Prozent?
Was sind 100% Sehschärfe? Eine Übereinkunft über diese Frage gibt es nicht. Zwar scheint rein rechnerisch 100% einer Sehschärfe von 1,0 zu entsprechen, doch nach allgemeinem Sprachgebrauch legt die Aussage “100%” nahe, es sei eine “volle” bzw. “normale” Sehschärfe gemeint. Wie oben dargelegt, beträgt die “normale” Sehschärfe jedoch bei jungen, augengesunden Probanden etwa 2,0, so dass 100% (bezogen auf Bogenminuten) nur der halben “normalen” Sehschärfe entspricht. Hinzu kommt, dass die Sehschärfe mit dem Alter abnimmt (Aulhorn and Harms 1970), so dass bei einem 80jährigen Probanden eine Sehschärfe von 0,5 “normal” sein kann (Slataper 1950).
0% Sehschärfe gibt es nicht. Auf Anhieb könnte man denken, 0% Sehschärfe sei ein angemessener Ausdruck für Blindheit. Auf einer logarithmischen Skala gibt es jedoch keinen Nullpunkt. Bei der Sehschärfe bringt dies den Vorteil, dass man auch noch weit unter dem Bereich von 0,1 numerisch differenzieren kann (Tabelle 1). Es wäre zu prüfen, in wieweit semiquantitative Bezeichnungen wie “Fingerzählen” sich damit erübrigen.
Aus diesen Überlegungen geht hervor, dass eine Angabe der Sehschärfe in % vermieden werden sollte.
Automatisierte Sehschärfebestimmung
Es gibt eine Reihe von Vorschlägen für eine automatisierte Sehschärfebestimmung (Crossman et al. 1970; Timberlake et al. 1980; Huber 1984; Friendly and Weiss 1985; Huber 1985; Wong and Plumb 1986; Raymond and Shapiro 1988; Effert et al. 1989; Strobel and Jacobi 1989; Diepes 1990; Ettelt et al. 1991; Huber 1992; Mittelviefhaus et al. 1993; Reading and Weale 1993; Lenne et al. 1994; Weigmann and Petersen 1996; Hautzinger and Haase 1997). Auch Computer-gestützte Verfahren müssen der EN ISO 8596 entsprechen. Dies ist z.B. beim “Freiburger Visustest” (Bach 1995; Bach 1996) der Fall, der vom Probanden selbständig bedient werden kann, ohne Vorinformation auskommt und den Untersuchereinfluss minimiert. Er ist im Internet frei verfügbar unter www.michaelbach.de/fract.html.
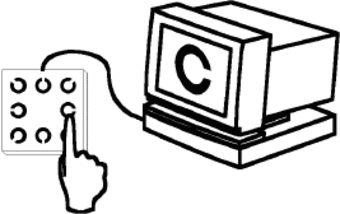
Abb. 3. “Freiburger Visustest”. Wenn ein Landoltring auf dem Computerbildschirm erscheint, reagiert der Proband durch Drücken einer von 8 Tasten. Die Tasten sind mit Landoltringen in den 8 möglichen Orientierungen gekennzeichnet und entsprechend angeordnet.
Auf einem Computerbildschirm erscheint jeweils ein Landoltring (Abb. 3). Durch Drücken einer entsprechenden Taste gibt der Proband die Position der Lücke an. Darauf folgt (optional) eine optische und/oder akustische Rückmeldung über die korrekte Lückenposition, und danach wird das nächste Sehzeichen angeboten. Begonnen wird immer mit einem großen Landoltring. Danach hängt die Größe des angebotenen Landoltrings von der Probandenantwort ab. Sie wird nach dem “best-PEST-Verfahren” (Lieberman and Pentland 1982) berechnet, mit dem man den Wendepunkt der psychometrischen Funktion sehr schnell bestimmt. Dabei geht man von einer vorgegebenen Steilheit der psychometrischen Funktion aus. Durch einen computergraphischen Trick (“Anti-aliasing”; Bach 1997) können in 5 m Abstand auch Sehschärfewerte über 2,0 mit feinen Abstufungen ermittelt werden, was sonst an der Pixelgröße normaler Bildschirme scheitern würde (Bach 1996; Bach et al. 1997). Um die bei jeder Schwellenbestimmung drohende Unlust des Probanden zu überwinden, wird bei jedem 6. Mal ein leicht erkennbarer Landoltring angeboten, der 3 mal so groß ist wie derjenige, der im jeweiligen Stadium der Prüfung dem wahrscheinlichsten Schwellenwert entspricht. Die Messzeit ist bei Erstuntersuchungen etwa halb so groß wie bei manueller Prüfung nach DIN bzw. EN ISO (Mittelviefhaus et al. 1993). Bei Wiederholungsuntersuchungen braucht man mit dem Freiburger Visustest aber etwas länger als mit dem manuellen Verfahren, da jedes Mal wieder mit einem großen Landoltring begonnen und das Vorergebnis nicht genützt wird. Andererseits hat sich gezeigt, dass sich Patienten, die mehrfach untersucht wurden, mit dem Freiburger Visustest schnell anfreunden. Viele Kinder sind von dem “Computerspiel” regelrecht begeistert.
Im Rahmen wissenschaftlicher Studien ist es oft nötig, die Sehschärfe verschiedener Probanden zu mitteln. Dabei wird zuweilen die arithmetische Mittelung angewandt. Dies ist jedoch nicht korrekt, da die den Empfindungsstufen angemessene logarithmische Skalierung der Sehschärfe nicht berücksichtigt wird; so wird z.B. der Abstand von 0,1 auf 0,2 gleich behandelt wie der von 1,0 auf 1,1.
Zum Mitteln der Sehschärfe gibt es zwei korrekte Methoden, die mathematisch identisch sind: die geometrische und die von uns hier als “logarithmisch” bezeichnete Mittelung. Der geometrische Mittelwert ist die n-te Wurzel aus dem Produkt der Einzelwerte. Bei der logarithmischen Mittelung muss man zuerst die einzelnen Sehschärfewerte logarithmieren, dann arithmetisch mitteln und schließlich den erhaltenen Wert “delogarithmieren” (=exponenzieren). Beide Verfahren sind mathematisch äquivalent und führen daher zum selben Ergebnis.
Der Fehler, der sich aus einer arithmetischen Mittelung ergibt, fällt dann besonders ins Gewicht, wenn die in die Mittelung eingehenden Werte weit auseinander liegen. Dies sei an einem Beispiel demonstriert. Nehmen wir an, ein und dieselbe Operationsmethode werde in zwei verschiedenen Kliniken durchgeführt. Beide Kliniken haben gleiche Ergebnisse, nämlich einen Patienten, bei dem die Sehschärfe von 1,0 auf 1,2 und einen anderen, bei dem sie von 0,1 auf 0,3 anstieg. Beim ersten Patienten hat sich die Sehschärfe um den Faktor 1,2 und beim zweiten um den Faktor 3 verbessert. Bei der Aufarbeitung der Ergebnisse mittelt Klinik A arithmetisch, Klinik G geometrisch.
Bei der unkorrekten arithmetischen Mittelung in der Klinik A ergibt sich:
- präoperativer Visus: (1,0+0,1)/2 = 0,55;
- postoperativer Visus: (1,2+0,3)/2 = 0,75.
Bei der korrekten logarithmischen Mittelung in der Klinik G ergibt sich:
- präoperativer Visus: (log(1,0) + log(0,1))/2 = (0+(-1))/2 = -0,5;
- Delogarithmierung: 100,5= 0,3;
- postoperativer Visus: (log(1,2) + log(0,3))/2 = (0,079 + (-0.52))/2 = -0,22;
- Delogarithmierung: 100,22 = 0,6.
Die Angabe der logarithmisch mittelnden Klinik G, dass sich die Sehschärfe von 0,3 auf 0,6 verbessert, also verdoppelt habe, gibt das “durchschnittliche Empfinden” der Patienten wesentlich besser wieder als die Angabe der arithmetischen mittelnden Klinik A, die nur über eine Verbesserung von 0,55 auf 0,75 berichtet, also um den Faktor 1,36.
Glücklicherweise ist der durch arithmetische Mittelung entstehende Fehler klein, wenn die eingegangenen Werte nur wenig streuen. Daher sind Studien, in denen arithmetisch gemittelt wurde, nicht unbedingt als obsolet zu verwerfen.
Die logarithmierten Sehschärfewerte sind in der Regel normal verteilt (Petersen 1993). Man kann sie daher nicht nur mitteln, sondern auch Streumaße berechnen, z.B. Standardabweichung (standard deviation, SD), Standardfehler des Mittelwertes (standard error of the mean, SEM = SD/Wurzel(n) oder Konfidenzintervalle. Bei der anschließenden Delogarithmierung ergeben sich dann nach oben und unten numerisch ungleiche Abstände zum Mittelwert. Bei graphischer Darstellung mit einer logarithmischen Skala sind die Streubalken aber wieder gleich lang.
Die Angabe eines Mittelwerts mit einer Abweichung von “±xx” kann also nicht korrekt sein. Ein Beispiel möge dies verdeutlichen. Wir nehmen folgenden Mittelwert auf der logarithmischen Skala an:
- log(mittlerer Visus) = -0,3 (entspricht einem Visus von 0,5).
Für den Standardfehler des Mittelwertes möge sich auf der logarithmischen Skala folgender Wert ergeben haben:
- log(SEM) = 0,1.
Um die Genauigkeit des Mittelwertes anzugeben, eignet sich das 95%-Konfidenzintervall, das gegeben ist durch den Mittelwert ± 1,96xSEM. Die untere Grenze dieses Bereichs sei mit kunten benannt, die obere mit koben.
Die Grenze kunten errechnet sich wie folgt:
- log(kunten) = log(mittlerer Visus) - 1,96log(SEM) = -0,3 - 0.2 = -0,5;
- kunten = 10-0,5 ~ 0,32.
Die Grenze koben errechnet sich wie folgt:
- log(koben) = log(mittlerer Visus) + 1,96log(SEM) = -0,3 + 0,2 = -0,1
- koben = 10-0,1 ~ 0,8.
Es ergibt sich also, ausgehend von der mittleren Sehschärfe 0,5, ein 95%-Konfidenzintervall für den Mittelwert von 0,32 bis 0,8. Diese nach oben und nach unten ungleichen Intervalle (0,18 und 0,3) transformieren sich jedoch in einer logarithmischen Abbildung wieder in gleichweite Abstände.
Eine weitere korrekte Möglichkeit für die Angabe der Streuung sind “Visusstufen” oder “Zeilen”. Sie berücksichtigen die logarithmische Skalierung der Sehschärfe und sind sehr anschaulich. Man muss die Visusstufe allerdings definieren, und zwar als Faktor 10. Wurzel aus 10 ~ 1,26.
Wenn log(Visus) in einer Patientengruppe nicht normal verteilt ist, muss man nichtparametrische (verteilungsfreie) statistische Verfahren verwenden. Da diese nur ein Ordinal-Skalenniveau voraussetzen, erübrigt sich jede Datentransformation, wie z.B. Logarithmieren. Gleichgültig, ob man Visus, log(Visus), MAR oder log(MAR) verwendet, bei der Statistik kommt dasselbe Ergebnis heraus.
Neuerdings wird in wissenschaftlichen Arbeiten das Auflösungsvermögen des Auges häufig mit “Minimum Angle of Resolution” = “MAR” angegeben. Es handelt sich dabei um den Kehrwert der Sehschärfe (bei Prüfung mit dem Landoltring entspricht MAR also genau der Lückengröße in Bogenminuten). Bei der Mittelung des Auflösungsvermögens wird dann der Logarithmus von MAR verwendet: “log(MAR)”. Das ist nach den obigen Ausführungen korrekt, denn aus
- MAR = 1/Sehschärfe
folgt
- log(MAR) = log(1/Sehschärfe)
bzw.
- log(MAR) = -log(Sehschärfe).
Damit sind log(MAR) und log(Sehschärfe) bis auf das Vorzeichen identisch (dieser Sachverhalt wird von Ferris et al. (1982) irreführend dargestellt). Das umgekehrte Vorzeichen führt jedoch dazu, dass die Angabe in log(MAR) unanschaulich ist. So steigt z.B. bei einer geglückten Operation die Sehschärfe von 0,5 auf 1,0 an, MAR fällt jedoch von 2,0 auf 1,0 ab. Daher plädieren wir dafür, das Auflösungsvermögen mit der Sehschärfe zu quantifizieren und MAR in der Regel nicht zu verwenden. (Höchstens in Fällen, in denen die Exzentrizitätsabhängigkeit des Auflösungsvermögens mit anderen Sehfunktionen verglichen werden soll, wie z.B. der Bewegungsempfindlichkeit, kann die Angabe in MAR sinnvoll sein, weil sich dabei lineare Abhängigkeiten von der Exzentrizität ergeben können.)
- Aulhorn E, Harms H (1970) Über die Untersuchung der Nachtfahreignung von Kraftfahrern mit dem Mesoptometer. Klin Mbl Augenheilk 157:843-873
- Bach M (1995) Der Freiburger Visustest - Automatisierte Sehschärfebestimmung. Ophthalmologe 92:174-178
- Bach M (1996) The “Freiburg Visual Acuity Test” - Automatic measurement of the visual acuity. Optometry & Vision Sci 73:49-53
- Bach M (1997) Anti-aliasing and dithering in the ‘Freiburg Visual Acuity Test’. Spatial Vision 11:85-89
- Bach M (1997) Raster-scan cathode ray tubes for vision research - limits of resolution in space, time and intensity, and some solutions. Spatial Vision 10:403-414
- CEN (1996) Europäische Norm Sehschärfeprüfung EN ISO 8596. Berlin, Beuth-Verlag
- Crosman E, Godeve P, Marg E (1970) A computer-based automatic method for determining visual acuity. Am J Optom 47:344-355
- Diepes H (1990) Erzeugung von Sehproben mit dem Computerbildschirm - Möglichkeiten und Grenzen. Optometrie 1:3-11
- Effert R, Steinmetz H, Jansen W, Ran G, Reim M (1989) Automatisierte Messung des Fernvisus in Anlehnung an die DIN-Strategie. Klin Mbl Augenheilk 195:39-43
- Ettelt B, Brando H, Zrener E, Lund 0 (1991) Visustestgerät: Möglichkeiten und Grenzen der LCD-Technik. Fortschr Ophthalmol 88:59-63
- Ferris FL, Kasof A, Bresnick GH, Bailey I (1982) New visual acuity charts for clinical research. Am J Ophthalmol 94:91-96
- Friendly DS, Weiss IP (1985) An automated visual acuity testing computer program using the Apple II system. Am J Ophthalmol 99:188-192
- Green DM, Swets JA (1966) Signal detection theory and psychophysics. New York, Wiley
- Harvey LO (1986) Efficient estimation of sensory tresholds. Behavior Research Methods, Instruments, Computers 18:623-632
- Hautzinger S, Hase W (1997) Fernvisusbestimmung nach DIN 58220 (Kriterium 6/10): Computersehtest mit hochauflösendem Monitor im Vergleich mit Sehtafeln. Klin Mbl Augenheilk 211:380-386
- Huber C (1984) Computergrafik für den Augenarzt. Klin Mbl Augenheilk 184:439-441
- Huber C (1985) Sehtest-Programm für Augenärzte auf Apple II, IIe und IIc Computer. Klin Mbl Augenheilk 186:227-230
- Huber C (1992) Prüfung der Sehfunktion mit Bildschirmgraphik auf dem Macintosh II Rechner. Klin Mbl Augenheilk 200:589-591
- Lenne RC, Vingrys AJ, Smith G (1994) Automated visual acuity testing. Clin and Exp Optom 77:190-195
- Lieberman HR, Pentland AP (1982) Microcomputer-based estimation of psychophysical thresholds: The best PEST. Behav Res Meth Instrum 14:21-25
- Mittelviefhaus K, Bach M, Jedynak A, Kommerell G (1993) Der Freiburger Visustest. Ophthalmologe 90:132-135
- Paliaga GP (1993). Die Bestimmung der Sehschärfe. München, Quintessenz-Verlag
- Petersen J (1990) Zur Fehlerbreite der subjektiven Visusmessung. Fortschr Ophthalmol 87:604-608
- Petersen J (1993) Fehlerhafte Visusbestimmungen und ihre quantitativen Auswirkungen. Ophthalmologe 90:533-538
- Rassow B, Cavazos H, Wesemann W (1990) Normgerechte Sehschärfenbestimmung mit Buchstaben. Augenärztliche Fortbildung 13:105-114
- Raymond JE, Shapiro KL (1988) Usefulness of computerized visual acuity testing in a pediatric ophthalmology clinic. Can J Ophthalmol 23:213-215
- Reading VM, Weale RA (1993) Self-administered automatic sight-testing. A feasibility study. Doc Ophthalmol 83:43-54
- Slataer FJ (1950) Age norms of refraction and vision. Arch Ophthalmol 43:466-479
- Strobel J, Jacobi F (1989) Automatische Prüfung von Sehfunktionen durch Computereinsatz. Fortschr Ophthalmol 86:370-373
- Timberlake GT, Mainster MA, Schepens CL (1980) Automated clinical visual acuity testing. Am J Ophthalmol 90:369-373
- Weinmann U, Petersen J (1996) DIN-kompatible Visusbestimmung höherer Reproduzierbarkeit mit Staircase-Messung und Maximum-likelyhood-Auswertung. Ophthalmologe 98:328-332
- Westheimer G (1979) Scaling of visual acuity measurements. Arch Ophthalmol 97:327-330
- Wong D, Plumb A (1986) Computer acuity testing for visual screening. Trans Ophthal Soc U.K. 105:498-503
Kontakt
Klinik für Augenheilkunde
Killianstraße 5
79106 Freiburg
Online unten auf der Patientenseite
Information: 0761 270-40010
Regelambulanz: 0761-270-40020 (9.00 bis 12.00 Uhr)
Privatambulanz: 0761-270-40150 (8.30 bis 13.30 Uhr)
E-Mail: augenklinik.terminvergabe@uniklinik-freiburg.de
Neuroophthalmologie / Kinder / Schielbehandlung: 0761-270-40440
Fax (Regel/Privat): 0761 270-41290
